In our studio project research we are using contracting shape memory alloy wires to bend frame panels.
Flexinol is a brand name for a specifically programmed shape memory alloy that contracts by 4.5% when heated to a specific temperature and then returns to its initial length. In our case, a flexinol wire connects two points of a planar frame, causing it to bend.

physical model
After physical testing of various frame materials, thicknesses, geometries and anchoring points of the flexinol, we decided to simulate the system’s behavior, using grasshopper and kangaroo.
The frame geometry we are simulating is the pentagon. The lower edge is anchored and the flexinol wire runs from 11 possible point positions on that edge, to 11 point positions on each of the two upper edges, as shown on the diagram.
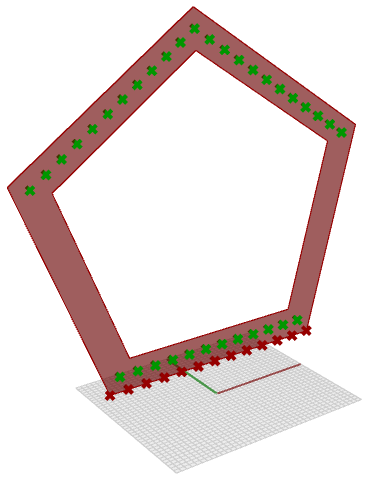
Flexinol anchor points
The parameters we set in our grasshopper definition are:
- The pentagon’s radius and frame’s offset distance
- The flexinol’s lower anchor point
- The Flexinol’s upper anchor point
- The frame’s stiffness
The optimization run by galapagos will give us the configuration with the maximum ratio of displacement / flexinol length.
Galapagos run more than three generations, from which point on it kept crushing, so the results are not pointing towards a specific configuration. At this point we decided to work with octopus for the optimization procedure.
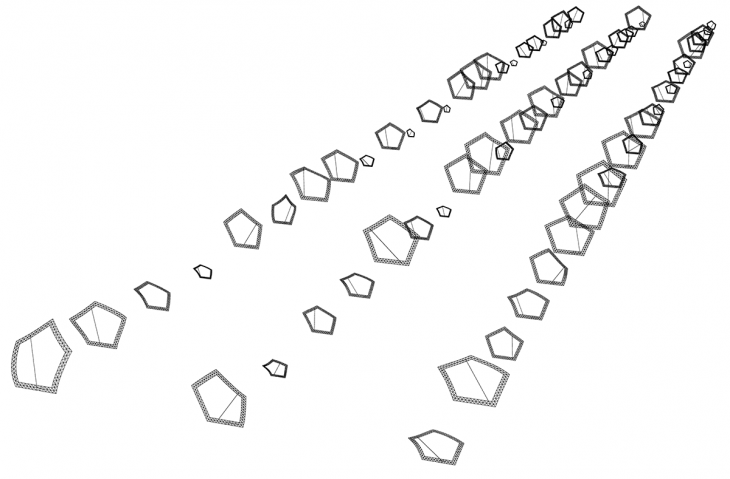
galapagos results
Working with octopus proved more stable, but still left us with lots of invalid configurations.
Octopus, nevertheless, let us organize the results on two axis, for the two main fitness parameters, the flexinol’s length and the frame’s displacement (in radians).
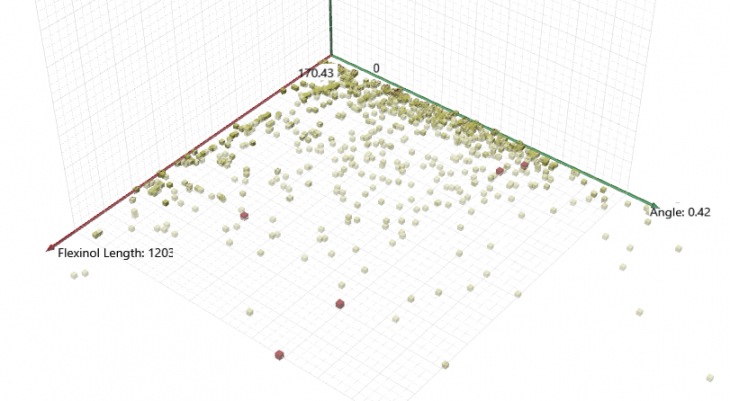
Octopus two-axis results visualization
By simplifying the parameters and reducing them to only control the anchor points, we get more specific and accurate results.
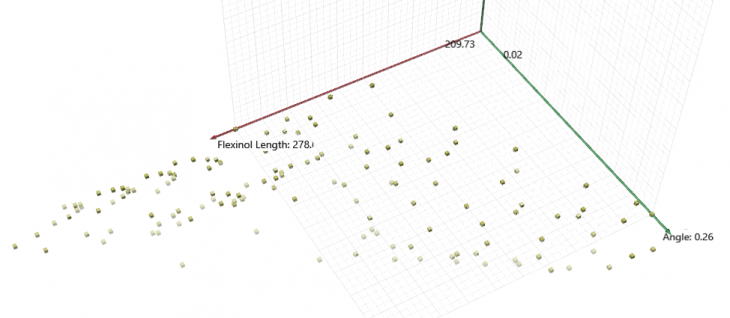
Octopus visualization of the simplyfied optimization
The optimum solutions can be seen on the “pareto front”, the configurations that give results closes to the optimum of the two axes. Each result can be selected and presented on grasshopper.
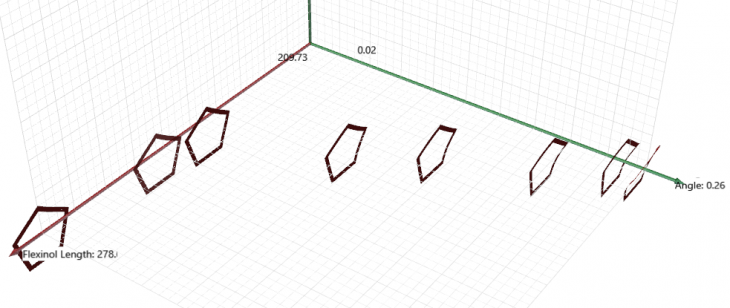
The “pareto front” with the optimum elite

The army of solutions given by octopus
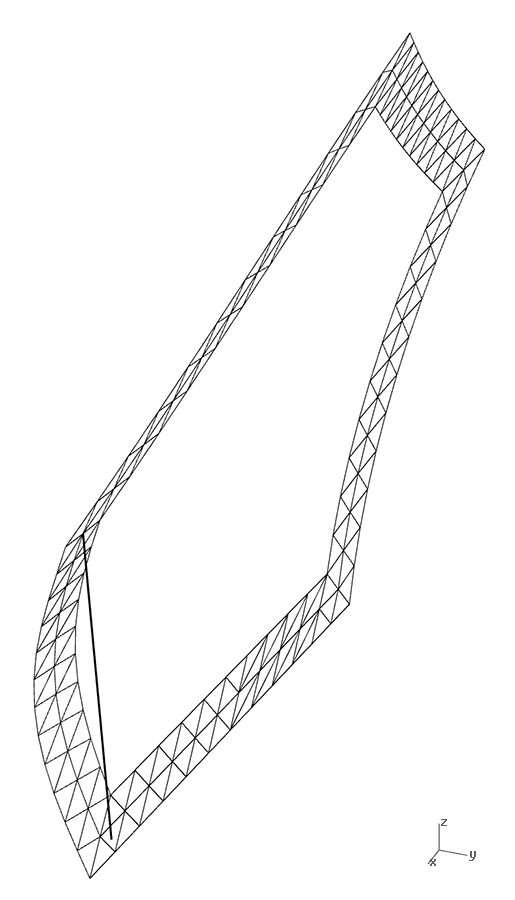
One of the optimum solutions
