HIGH DENSITY ENERGY STORAGE USING SELF-ASSEMBLED MATERIALS
The assignment is related to our methane research for the Self Sufficient studio. The challenge of this exercise is to propose an approach in theoretical design of material at the atomic scale that can maximize the amount of stored of methane in a given volume. The methane molecules are attracted to surfaces, while being repelled from each other. We attempt to simulate the interaction between methane and the Calabi-Yau surface area of a hypothetically ideal “methane-catching” material in a sample volume (scale of a methane molecule: pico meters).
___________INTRO
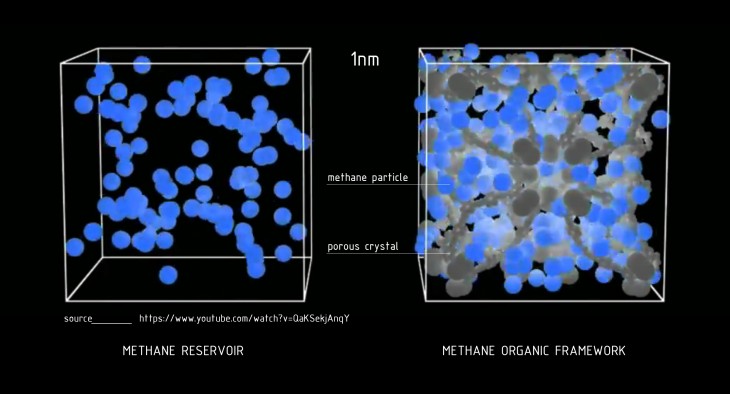
Porous crystals (Metal-Organic Frameworks) are excellent materials for natural gas storage due to their nanoscopic pores and incredibly high surface area. The script generates hypothetical metal-organic frameworks (MOFs), visualizing the most promising structures. MOFs then can be synthesized and tested in the laboratory conditions.
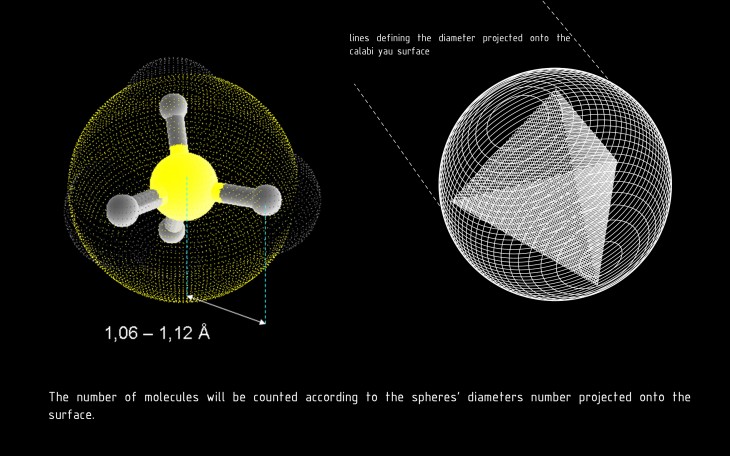
A Calabi-Yau space is used by physicists to describe parts of nature that are too small to see with naked human eye. It is believed, that matter is composed of atoms, and the distances between the components of the atoms are measured at 0.000000000000001 meters (pico meters). Methane CH4 is comprised of one atom of carbon and four atoms of hydrogen. The diameter of the entire molecule is 398.8 pico meters. In the script we will be attempting to optimize the population of CH4 molecules attracted to the surface while ignoring the molecules free floating in-between.
___________DISCRETIZATION
The geometrical structure of methane molecule is a tetrahedron. Since a tetrahedron can be inscribed into a sphere, we are using later geometry in our optimization. The number of molecules will be counted according to the spheres’ diameter, projected onto the surface.
___________LOGIC
\\find the bounding box of the mesh
\\populate the bounding box with a 3dimensional diagrid of spheres that are their own radius’s distance from their neighbour
\\find which spheres collide with the mesh
\\cull all spheres that do not collide
\\run galapagos in different surface and angle configurations
___________ITERATIONS
Using galapagos we generated different options according to our variables in the solution space.